KTH framework for Nek5000 toolboxes; testing version  0.0.1
Files | Functions
Math
Framework for Nek5000 toolboxes » Toolbox » Utility module

Diverse tools for matht or data operations. More...

+ Collaboration diagram for Math:

Files

file  math_tools.f
 Set of math related tools for KTH modules.
 

Functions

real function math_stepf (x)
 Step function. More...
 
real function math_ran_dst (ix, iy, iz, ieg, xl, fcoeff)
 Give random distribution depending on position. More...
 
real function math_ran_rng (lower, upper)
 Give random number in the defined range. More...
 
real function math_zbqlu01 ()
 Marsaglia-Zaman random number generator. More...
 
subroutine math_zbqlini (seed)
 Initialise Marsaglia-Zaman random number generator. More...
 
subroutine math_edgind (istart, istop, iskip, iedg, nx, ny, nz)
 Give bounds for loops to extract edge of a 3D element. More...
 
subroutine math_etovec (vec, edg, vfld, nx, ny, nz)
 Extract 3D element edge. More...
 
subroutine math_rot3da (vo, vi, va, an)
 3D rotation of a vector along given axis. More...
 

Detailed Description

Diverse tools for matht or data operations.

Set of math related routines for toolbox

Module interface:
Global interface list:
Interface provided:
  1. math_stepf
  2. math_ran_dst
  3. math_ran_rng
  4. math_zbqlu01
  5. math_zbqlini
  6. math_edgind
  7. math_etovec
  8. math_rot3da

Function Documentation

◆ math_edgind()

subroutine math_edgind ( integer  istart,
integer  istop,
integer  iskip,
integer  iedg,
integer  nx,
integer  ny,
integer  nz 
)

Give bounds for loops to extract edge of a 3D element.

Note
All edge related routines used IXCN and ESKIP, but this caused some problems as these arrays have to be continuosly updated for different levels in pressure solver, so I add this routine.
Parameters
[out]istartlower loop bound
[out]istopupper loop bound
[out]iskipstride
[in]iedgedge number
[in]nx,ny,nzelement size

Definition at line 252 of file math_tools.f.

+ Here is the caller graph for this function:

◆ math_etovec()

subroutine math_etovec ( real, dimension(nx)  vec,
integer  edg,
real, dimension(nx*ny*nz)  vfld,
integer  nx,
integer  ny,
integer  nz 
)

Extract 3D element edge.

Note
This routine works on singe element not the whole field.
Parameters
[out]vecvector containg edge values
[in]edgedge number
[in]vfldpointer to singe element in the field
[in]nx,ny,nzelement size

Definition at line 298 of file math_tools.f.

References math_edgind().

+ Here is the call graph for this function:
+ Here is the caller graph for this function:

◆ math_ran_dst()

real function math_ran_dst ( integer  ix,
integer  iy,
integer  iz,
integer  ieg,
real, dimension(ldim)  xl,
real, dimension(3)  fcoeff 
)

Give random distribution depending on position.

The original Nek5000 random number generator is implementted in ran1. This totally ad-hoc random number generator below could be preferable to the original one for the simple reason that it gives the same initial cindition independent of the number of processors, which is important for code verification.

Parameters
[in]ix,iy,izGLL point index
[in]iegglobal element number
[in]xlphysical point coordinates
[in]fcoefffunction coefficients
Returns
random distribution

Definition at line 54 of file math_tools.f.

◆ math_ran_rng()

real function math_ran_rng ( real  lower,
real  upper 
)

Give random number in the defined range.

Parameters
[in]lower,upperrange for random numer
Returns
random number in the defined range

Definition at line 81 of file math_tools.f.

References math_zbqlu01().

+ Here is the call graph for this function:

◆ math_rot3da()

subroutine math_rot3da ( real, dimension(ldim)  vo,
real, dimension(ldim)  vi,
real, dimension(ldim)  va,
real  an 
)

3D rotation of a vector along given axis.

Parameters
[in]vooutput vector
[in]viinput vector
[in]varotation axis
[in]anrotation angle

Definition at line 331 of file math_tools.f.

References copy().

+ Here is the call graph for this function:
+ Here is the caller graph for this function:

◆ math_stepf()

real function math_stepf ( real  x)

Step function.

Continuous step function:

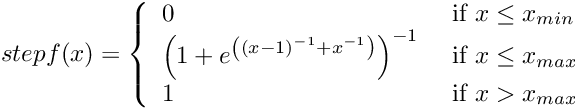
\begin{eqnarray*} stepf(x) = \left\{ \begin{array}{ll} 0 &\mbox{ if $x \leq x_{min}$} \\ \left(1+e^{\left((x-1)^{-1} + x^{-1}\right)}\right)^{-1} &\mbox{ if $x \leq x_{max}$} \\ 1 &\mbox{ if $x > x_{max}$} \end{array} \right. \end{eqnarray*}

with $ x_{min} = 0.0001$ and $ x_{max}=0.9999$

Parameters
[in]xfunction argument
Returns
math_stepf

Definition at line 20 of file math_tools.f.

◆ math_zbqlini()

subroutine math_zbqlini ( integer  seed)

Initialise Marsaglia-Zaman random number generator.

To initialise the random number generator - either repeatably or nonrepeatably.

Parameters
[in]seednumber which generates elements of the array ZBQLIX
Todo:
Remove all common blocks and save variables to make it possible to be used by multiple tools

Definition at line 179 of file math_tools.f.

+ Here is the caller graph for this function:

◆ math_zbqlu01()

real function math_zbqlu01

Marsaglia-Zaman random number generator.

Returns a uniform random number between 0 & 1, using a Marsaglia-Zaman type subtract-with-borrow generator.

Remarks
Uses double precision, rather than integer, arithmetic throughout because MZ's INTEGER constants overflow 32-bit INTEGER storage (which goes from -2^31 to 2^31). Ideally, we would explicitly truncate all INTEGER quantities at each stage to ensure that the DOUBLE PRECISION representations DO not accumulate approximation error; however, on some machines the USE of DNINT to accomplish this is seriously slow (run-time increased by a factor of about 3). This DOUBLE PRECISION version has been tested against an INTEGER implementation that uses long integers (non-standard and, again, slow) - the output was identical up to the 16th decimal place after 10^10 calls, so we're probably OK ... In current implementation we follow Nek5000 compilation rulles prolonging all reals to doulbe with compiler flaggs.
Author
Richard Chandler (richa.nosp@m.rd@s.nosp@m.tats..nosp@m.ucl..nosp@m.ac.uk)
Paul Northrop (north.nosp@m.rop@.nosp@m.stats.nosp@m..ox..nosp@m.ac.uk)
Returns
random number
Todo:
Remove all common blocks and save variables to make it possible to be used by multiple tools

Definition at line 119 of file math_tools.f.

+ Here is the caller graph for this function: